
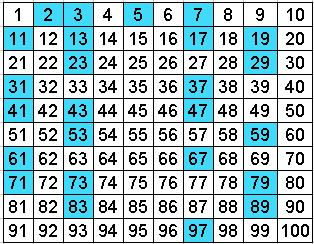
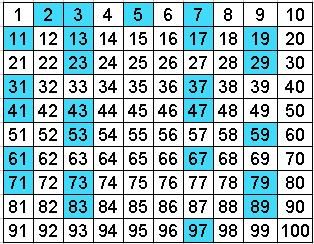
These are the primes which are less than the square root of 100, i.e. You may have noticed that all composite numbers in the grid above (the crossed-out numbers) are divisible by 2, 3, 5 or 7. but P(41) is equal to 41 2, so P(41) is not prime. But they are still intrigued by formulae which can generate some of the primes, for example:ġ) In 1772 Euler noticed that the quadratic polynomial P(n) = n 2 - n + 41 is prime for all positive integers n less than 41. Most mathematicians do not expect such a formula to exist.

Many people have tried and failed to find a simple formula for generating all of the prime numbers.Prime numbers are rather mysterious, and they have intrigued mathematicians through the ages.
We have already used this theorem: In the first mini-challenge, we saw that the total number of divisors is related to the (unique) prime factorization in a simple way. Although the order of the primes in the product is arbitrary, the primes themselves are not. The " Fundamental Theorem of Arithmetic", established by Euclid, says that:Įvery integer greater than 1 is either prime itself or is the product of prime numbers.

Every number is built out of prime factors, just as every molecule is built out of atoms. Prime numbers can be thought of as the "building blocks" of the whole numbers. Split into a product of primes in just one way (if we don't worry about the order of multiplication).


 0 kommentar(er)
0 kommentar(er)
